Integral de Lebesgue


La integral de Riemann no está definida para un ancho abanico de funciones y situaciones de importancia práctica (y de interés teórico). Por ejemplo, la integral de Riemann puede integrar fácilmente la densidad para obtener la masa de una viga de acero, pero no se puede adaptar a una bola de acero que se apoya encima. Esto motiva la creación de otras definiciones, bajo las cuales se puede integrar un surtido más amplio de funciones.8 La integral de Lebesgue, en particular, logra una gran flexibilidad a base de centrar la atención en los pesos de la suma ponderada.
Así, la definición de la integral de Lebesgue empieza con una medida, μ. En el caso más sencillo, la medida de Lebesgue μ(A) de un intervalo A = [a, b] es su ancho, b − a, así la integral de Lebesgue coincide con la integral de Riemann cuando existen ambas. En casos más complicados, los conjuntos a medir pueden estar altamente fragmentados, sin continuidad y sin ningún parecido a intervalos.
Para explotar esta flexibilidad, la integral de Lebesgue invierte el enfoque de la suma ponderada. Como expresa Folland:9 "Para calcular la integral de Riemann de f, se particiona el dominio [a, b] en subintervalos", mientras que en la integral de Lebesgue, "de hecho lo que se está particionando es el recorrido de f".
Un enfoque habitual define primero la integral de la función característica de un conjunto medible A por:
\int 1_A d\mu = \mu(A).
Esto se extiende por linealidad a las funciones escalonadas simples, que sólo tienen un número finito n, de valores diferentes no negativos:
\begin{align} \int s \, d\mu &{}= \int\left(\sum_{i=1}^{n} a_i 1_{A_i}\right) d\mu \\ &{}= \sum_{i=1}^{n} a_i\int 1_{A_i} \, d\mu \\ &{}= \sum_{i=1}^{n} a_i \, \mu(A_i) \end{align}
(donde la imagen de Ai al aplicarle la función escalonada s es el valor constante ai). Así, si E es un conjunto medible, se define
\int_E s \, d\mu = \sum_{i=1}^{n} a_i \, \mu(A_i \cap E) .
Entonces, para cualquier función medible no negativa f se define
\int_E f \, d\mu = \sup\left\{\int_E s \, d\mu\, \colon 0 \leq s\leq f\text{ y } s\text{ es una funcion escalonada}\right\};
Es decir, se establece que la integral de f es el supremo de todas las integrales de funciones escalonadas que son más pequeñas o iguales que f. Una función medible cualquieraf, se separa entre sus valores positivos y negativos a base de definir
\begin{align} f^+(x) &{}= \begin{cases} f(x), & \text{si } f(x) > 0 \\ 0, & \text{de otro modo} \end{cases} \\ f^-(x) &{}= \begin{cases} -f(x), & \text{si } f(x) < 0 \\ 0, & \text{de otro modo} \end{cases} \end{align}
Finalmente, f es Lebesgue integrable si
\int_E |f| \, d\mu < \infty , \,\!
y entonces se define la integral por
\int_E f \, d\mu = \int_E f^+ \, d\mu - \int_E f^- \, d\mu . \,\!
Cuando el espacio métrico en el que están definidas las funciones es también un espacio topológico localmente compacto (como es el caso de los números reales R), las medidas compatibles con la topología en un sentido adecuado (medidas de Radon, de las cuales es un ejemplo la medida de Lebesgue) una integral respecto de ellas se puede definir de otra manera, se empieza a partir de las integrales de las funciones continuas con soporte compacto. De forma más precisa, las funciones compactamente soportadas forman unespacio vectorial que comporta una topología natural, y se puede definir una medida (Radon) como cualquier funcional lineal continuo de este espacio; entonces el valor de una medida en una función compactamente soportada, es también, por definición, la integral de la función. Entonces se continúa expandiendo la medida (la integral) a funciones más generales por continuidad, y se define la medida de un conjunto como la integral de su función característica. Este es el enfoque que toma Bourbaki10 y cierto número de otros autores. Para más detalles, véase medidas de Radon.

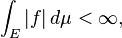
No hay comentarios:

Publicar un comentario

Suscribirse a: Entradas (Atom)